Présentation de la suite de logiciels mecaflux:
Modelisation helice aerienne dans heliciel
Modelisation helice bateau dans heliciel
Modelisation helice ventilation dans heliciel
Modelisation helice eolienne dans heliciel
Modelisation hydrolienne dans heliciel
Modelisation helice kaplan dans heliciel
Theorie de Froude relative aux hélices de traction ou propulsion
- Pour comprendre ce qui suit la notion de quantité de mouvement doit etre maitrisée, car c'est sur le bilan de quantité de mouvement que la théorie de Froude s'appuie..
- l'approche de froude nous permet d'évaluer la vitesse induite axiale en utilisant un volume de controle autour de la veine de fluide traversant l'hélice. En calculant le volume de fluide devant pénétrer le volume de controle latéralement, du fait de la contraction de la veine de fluide engendrée par l'augmentation de la vitesse produite par l'hélice: Suivant l'approche proposée par Froude, on peut considérer l'hélice comme un disque uniformément chargé ayant un nombre infini de pales (fig. 1). De plus, on pose les hypothèses suivantes, selon lesquelles
- on ne tient pas compte de la rotation de l'écoulement.
- on considere une veine fluide en dehors de laquelle l'écoulement ne connait pas de perturabation.
- La pression à l'infini amont et aval est égale a la pression statique de l'écoulement non perturbé
- Les perturbation de l'air sont suffisament faibles pour que l'on suppose que la densité du fluide est constante.
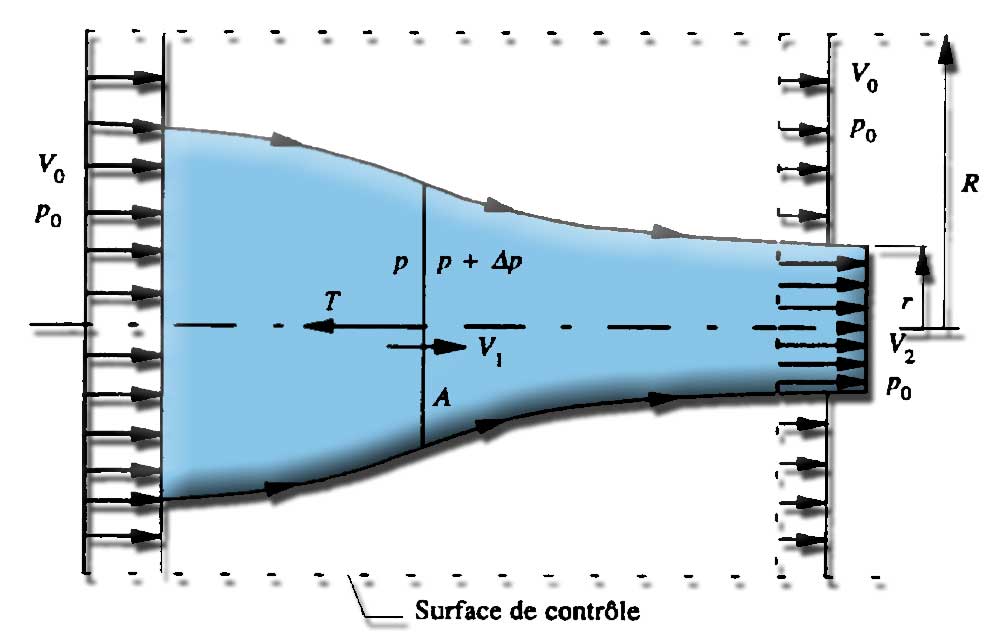 fig. 1
fig. 1
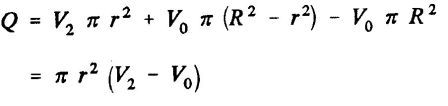
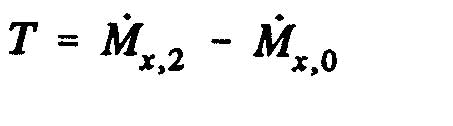
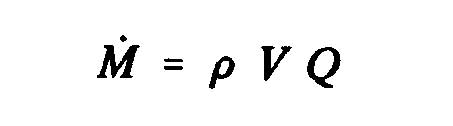
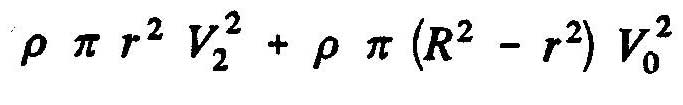
![]()
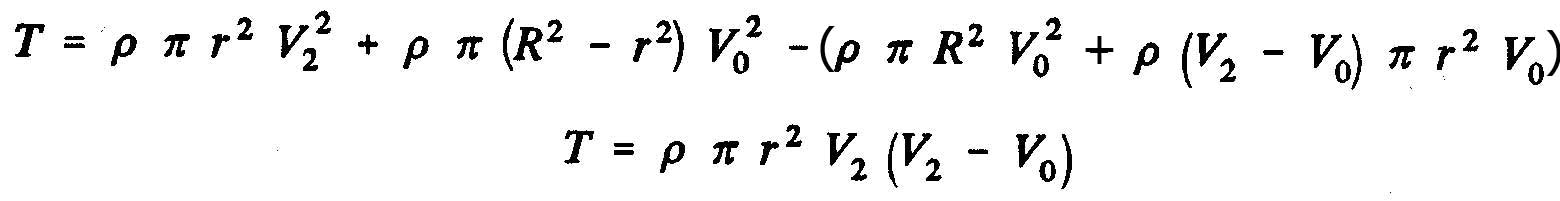
![]()
![]()
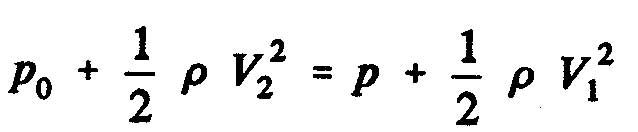
La différence de pression statique entre les faces aval et amont du disque de l'hélice a comme expression
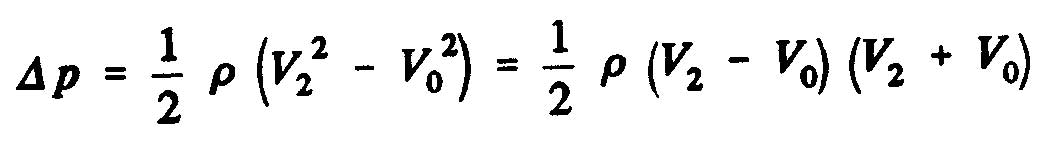
![]()
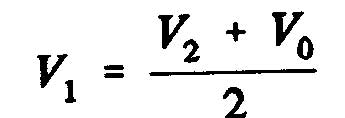
On appelle vitesse induite, w, l'augmentation de vitesse au niveau du disque de l'hélice:
![]()
![]()
Maintenant, si on tient compte de l'expression:
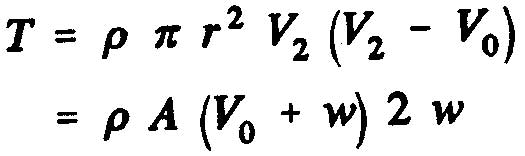
De cette expression de la poussée nous pouvons dégager la notion de débit massique: La masse de fluide traversant l'hélice par seconde est :
- (kg/sec) m = rho.pi.r².V2
avec rho= masse volumique en kg/m3 r= rayon en bout de pale et pi=3.14
Nous voyons donc que la force de poussée ou de traction de l'hélice est T=m.(v2-v0)- Il est important de constater que créer de la poussée, consiste donc à augmenter la vitesse d'un debit massique de fuide. Ceci met en evidence les leviers dont nous disposons pour génerer la force de propulsion: Le choix d'agir sur la masse ou la variation de vitesse est déterminant pour le rendement propulsif
References bibliographique helice

 Carte et index global
Carte et index global Mecaflux
Mecaflux Didacticiels Pro3D
Didacticiels Pro3D Didacticiels Heliciel
Didacticiels Heliciel Boutique
Boutique Comparer fonctions des logiciels
Comparer fonctions des logiciels Devis, Commandes, Moyens de paiements
Devis, Commandes, Moyens de paiements Etudes projet
Etudes projet Formations logiciels
Formations logiciels